Летали ли американцы на Луну?

2. Фотографии и фотографирование

2.2.1. О направлениях лучей, длинах теней и прочем

2.2.2. Анализируй это!

Солнце на этой фотографии светит прямо в спину фотографу, однако тень от лунного модуля страдает левым уклонизмом. В ещё большей степени это относится к камням в правой части изображения, которые явно освещены справа. Этот эффект постепенно сходит на нет по мере перемещения к левой части изображения. Не могут ваши «неровности поверхности» настолько изменить направление теней!

Свет перемещается по прямым, параллельным линиям в любой данный момент. Теневые направления параллельны, потому что свет исходит из Солнца с расстояния в более чем 90 миллионов миль.

(В. Ростов, «Секретные исследования», http://skyzone.al.ru/space/usa_moon.html )

Одним из распространённейших и одновременно абсурднейших заблуждений в отношении лунных фотографий является то, что линии, параллельные «на натуре», якобы должны сохранять свою параллельность и на фотографии. В то же время, при рассмотрении «земных» фотографий в это заблуждение люди впадают достаточно редко. Никого, например, не удивляет, что параллельлные рельсы на снимках сходятся к горизонту, а снятый сбоку фасад дома вовсе не похож на прямоугольник, хотя крыша у него параллельна земле, а стены параллельны между собой. Ниже приведены фотографии сходящихся рельс и дома на Невском проспекте. Рядом с ними — фотография НАСА AS14-68-9486, часто приводимая «заговорщиками» в качестве примера разнонаправленных теней; жёлтыми линиями отмечены сходящиеся направления перспективы.

Важно! Явление, вызывающее изменение направления линий в кадре — это обыкновенная перспектива, та самая, которой учат в школе на уроках рисования.

Геометрическое объяснение перспективы состоит в том, что любая оптическая система характеризуется некоторым уголом зрения (горизонтальным и вертикальным, в случае лунных камер оба были равны 53,5^o). Рисунок с сайта http://www.clavius.org иллюстрирует концепцию поля зрения. Объекты, расположенные в правом и в левом краях кадра, находятся на угловом расстоянии 53,5^o/2=27^o от направления вертикальной линии, проходящей через центр кадра.
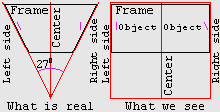Наш схематический рисунок (проекция поля зрения на горизонтальную плоскость) показывает, что истинная картина в кадре деформируется: края кадра, представляющиеся нам параллельными, на самом деле наклонены между собой на 53,5^o, так что передний план существенно уже заднего плана. Левая половина рисунка показывает, как формируется кадр, правая — кадр, как мы его видим на плёнке. Аналогичная картина, конечно же, наблюдается и в вертикальной плоскости. Объект на краю кадра, наклонённый на самом деле к центральной линии, представляется нам на фотографии параллельным центральной линии кадра. Объект, кажущийся на снимке наклонённым относительно центральной линии кадра, на самом деле может оказаться параллельным этой линии или даже наклонённым в противоположную сторону.

На вышеприведённом снимке модуля тень фотографирующего находится близко к левому углу снимка, а значит, в действительности наклонена влево от центральной вертикали кадра на ~20^o. Так что и без точных геометрических расчётов мы можем сделать вывод, что на самом деле обе тени, модуля и астронавта, наклонены в одну сторону — влево.

Сделанные построения относятся к идеальному объективу. На самом деле реальный объектив, тем более с таким широким полем зрения, как у лунных камер, вносит в изображения ряд дисторсий — дополнительных искажений поля зрения. Дисторсии особенно сильны по краям снимков и могут превышать 10 %. Они вносят дополнительный вклад в изменение углов на снимках.

Как видно, элементарный анализ снимка с модулем и тенью астронавта заставляет опровергнуть поспешный вывод о том, что солнце якобы светит в прямо спину фотографу. Вовсе нет. Солнце светит в спину и слегка справа от фотографа, так что его тень, как и тень модуля, наклонена влево относительно нижнего края фотографической плоскости градусов на двадцать. Только благодаря перспективе изображение тени становится параллельным боковым краям фотографии.

Почему же на некоторых снимках параллельные «на натуре» предметы сохраняют параллельность?

Посмотрите на <...> фотографию: типичные тени дерева. Проведите виртуальные параллельные линии теней — им совпадает теневая сторона деревьев. Никаких особенностей. Это и не удивляет.

(В. Ростов, «Секретные исследования», http://skyzone.al.ru/space/usa_moon.html )

Разумеется, в некоторых условиях тени могут сохранять параллельность. Во первых, перспективному искажению не подвержены линии, перпендикулярные оси объектива. Во вторых, всё зависит от того, как снимают и чем снимают. Если угол зрения камеры мал (например, при съёмке длиннофокусным объективом), то угловое расстояние между краями кадра невелико, и перспективное расхождение параллельных линий может быть малозаметным. Того же можно добиться, если вырезать небольшой фрагмент из фотографии, снятой широкоугольником: в пределах достаточно маленького фрагмента перспективные эффекты малы. Очевидно, предлагаемый снимок снят длиннофокусным объективом или представляет из себя фрагмент более крупного кадра. Кстати, и на нём перспективные эффекты имеют место: жёлтые линии не вполне параллельны теням деревьев, а последние, в свою очередь, слегка сходятся к горизонту.

Перспективой объясняются различные длины и направления теней, приводимых и на других фотографиях в статье Ростова (изображения 2, 3, 4, 5, 6, 10).

На «перспективные грабли» наступают не только при анализе теней, с натолкнуться на них можно и в других местах.

Видимо критики доконали NACA. Постоянные насмешки над тем, что ни одна из шести "лунных" экспедиций американцев не привезла фотографии Земли, снятой с Луны, вынудили NACA дать в немецкий журнал History (N2/2000) фото, на котором видна Земля. Но вот ведь умственные уроды! Астронавт освещён "солнцем" справа, а "Земля" — вертикально сверху! Ну что стоило "Землю" развернуть на 90^o?

(Ю. И. Мухин, газета «Дуэль», http://www.duel.ru/200031/?31_4_1 )

Проигнорируем целый ряд второстепенных ошибок, допущенных в столь коротком пассаже. Разумеется, астронавтов на Луну отправляло не NACA, а НАСА (NASA). Разумеется, из всех лунных экспедиций было привезено множество снимков Земли (об этом ниже). Даже сама представленная в газете фотография есть лишь зеркальное отражение подлинного снимка, а именно http://www.hq.nasa.gov/office/pao/History/alsj/a17/as17-134-20384.jpg Покажем лишь, почему на снимке всё на месте, и кто проявил себя «умственным уродом».

Увидев, что освещающие астронавта лучи падают под углом к краю кадра, справа налево, Мухин решил, что «астронавт освещён "солнцем" справа». Однако астронавт находится у границы кадра, которая, как мы уже выяснили выше, сама наклонена к центральной вертикали кадра на 27^o вправо. Чтобы определить истинный угол падения лучей в правой части снимка по отношению к вертикали кадра, следует вычесть из видимого угла между лучами и правой границей кадра те самые 27^o (см. схему выше, объект справа). Как видно, эта разность близка к 0^o — астнонавт освещён лучами, практически перпендикулярными плоскости кадра. Изображение Земли тоже развёрнуто к вертикали несколько больше, чем на самом деле; вероятно, в действительности терминатор Земли (линия раздела дня и ночи) перпендикулярен центральной вертикали.

Как видно, разоблачителю «умственных уродов» Мухину не пришло в голову учесть перспективное искажение. На самом деле солнце находится почти точно посзади фотографа, и на снимке всё в полном порядке. (Сколь далёк Мухин от понимания перспективы, он продемонстрирует ещё не раз.)

Может возникнуть вопрос: раз солнце находится позади фотографа, оно, казалось бы, должно освещать Землю «в лоб», так что мы должны видеть полный диск Земли? Опять-таки, нет. Во-первых, солнце светит не просто сзади, а сзади-сверху, как это видно по фигуре астронавта и по флагу. Во-вторых, нельзя забывать про вертикальную перспективу. Земля расположена в верхней части кадра, а значит, истинный угол терминатора с центральной горизонталью кадра на ~25^o больше кажущегося (кажущийся угол чуть больше 0^o, может быть, градусов десять — терминатор почти параллелен горизонтали). Если солнце выше горизонтали кадра на ~65^o, то оно освещает Землю под углом ~65^o+25^o=100^o — как раз то, что мы видим на снимке. (Всё это лишь грубые оценки, для точного определения нужен более глубокий анализ).

А давайте измерим отношение нижний части опоры спускаемого модуля к его верхней части. Получается приблизительно <...> 1:1. Теперь давайте достроим недостающую часть опоры на картинке. Мы знаем, что отношение верхний и нижний части <...> 1:1. Измерив размеры тарелки, на которую опирается нога, мы получим соотношение 1:0.9. Теперь, зная размеры ноги, мы можем ее достроить на правой части картинки. И, поскольку наши построения приблизительные, она может входить в картинку или не входить, но тень от нее должна быть на картинке обязательно. Четкая черная тень!

(http://iss.h1.ru/n0003.htm )

Похоже, уродливость получившейся «реконструкции» нимало не обеспокоила «реконструктора». Во-первымх, опоры модуля телескопические и, следовательно, все разной длины (чтобы адаптироваться к неровностям и сохранить вертикальное положение модуля), так что сама попытка оценить отношения длин обречена. Но главное — всё та же перспектива. «Реконструируемая» опора направлена от нас, поэтому её верхняя часть на несколько метров ближе к нам, чем нижняя — прямой путь к появлению перспективных эффектов. Что получится, если мы попробуем «реконструировать», без учёта перспективы, фрагмент вышеприведённого дома — просто механически перенеся вправо кусок близлежащей стены? Правильно, безобразие получится. Более далёкий от нас фрагмент должен быть на снимке визуально меньше более близкого фрагмента. То же и с опорой. Реконструируемый кусок должен быть короче. И тень от него имеется на снимке — как раз там, где она должна быть, несколько выше реконструкции.

Воспользуемся несколькими фотографиями, чтобы на их примере показать, как следует интерпретировать снимки с учётом эффектов перспективы.

Все дальнейшие вычисления приблизительны: мы пренебрегаем наклоном кадров к горизонту, перспективой в пределах небольших фрагментов кадра (фигуры астронавтов, опоры), дисторсией поля зрения в широкоугольном объективе. Измерения носят лишь оценочный характер. Тем не менее, погрешности наших оценок (порядка десятка процентов) несравненно ниже, чем у многих доморощенных и импортных «интерпретаторов».

Две фотографии астронавта Ф.Олдрина "на Луне" из журнала "Америка" (№162 апрель 1970 года) на фоне одной и той же опоры посадочного модуля "Аполлона-11". На первом снимке рост Ф.Олдрина оказывается равным приблизительно 2,5 метра, а на втором — 1,3 метра, или почти в два раза меньше...

(Л. Бацура, «Космическая нестыковка», http://www.zavtra.ru/cgi/veil/data/zavtra/01/388/72.html )

Полноразмерный цветной вариант снимков, приводимых Бацурой, можно легко найти на сайте НАСА. Воспользуемся картой места высадки. Первый снимок Бацуры — это кадр AS11-40-5872 , второй снимок — кадр AS11-40-5902 . Попробуем определить расстояния до Олдрина и длину опор на обоих снимках. Начнём с Олдрина.

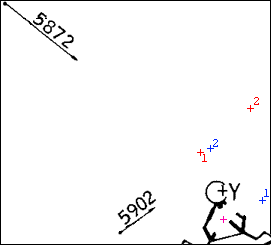Измерив расстояние на карте (линейка-шкала расстояний прилагается, 10 метрам соответствует отрезок приблизительно 235 пикселей; все измерения сделаны с помощью «Adobe Photoshop»), получим, что в первом случае расстояние от фотографа до центра опорной тарелки было 12 м, во втором — 4,5 м. Полная ширина 1-го снимка — около 440 пикселей, это соответствует 53 градусам (ширина поля зрения камеры). Высота Олдрина на этом снимке — 86 пикселей. Иными словами, Олдрин занимает в кадре угол 53^o*86/440=10,4^o и находится практически на одной линии с опорой. Аналогично находим, что во втором кадре Олдрин занимает 53^o*118/440=14,2^o; здесь его расстояние от центральной вертикали кадра около 60 пикселей, или 7,2^o. Предположим, вопреки Бацуре и во славу здравого смысла, что высота Олдрина в обоих случаях одинакова, и положим эту высоту равной 1,9 м. Найдём тогда, что в первом кадре Олдрин удалён от фотографа на расстояние 1,9/2*ctg(10,4/2)=10,4 м, а во втором кадре — на 1,9/2*ctg(14,2/2)=7,6 м. Нанесём на карту положения Олдрина на обоих снимках (красные кресты). Одновременно синими крестами обозначим положения Олдрина, если бы его высота была такой, как предлагает Бацура.

Как видно, если бы в первом кадре Олдрин действительно был бы так высок, как полагает Бацура, он оказался бы далеко за опорой — довольно нелепый результат. Возможно, Бацура сомневается, что в этом кадре между Олдрином и опорой всего лишь 1,8 м — но какие у него на то основания? Во втором кадре, по предположению Бацуры, расстояние между Олдрином и тарелкой не 3,8 м, как на самом деле, а 1,8 м — на 2 м меньше. Мы согласны — измеренное линейкой на фотографии, это расстояние действительно может показаться маленьким (близким к высоте Олдрина). Но не будем забывать про пресловутую перспективу и про то, что в отсутствие ориентиров (детали на фотографии, лежащие между Олдрином и тарелкой опоры, различить практически невозможно) оценивать «на глаз» расстояния по двухмерной перспективной проекции — почти безнадёжное дело. О трудностях определения расстояний писал и Армстронг (на странице в самом низу, раздел «Важно!»), причём имея в виду даже не фотографии, а собственно лунный ландшафт.

Займёмся теперь опорами. Правда, здесь расчёты грубее, чем при нахождении положений Олдрина.

В первом кадре высота проекции посадочной опоры на плоскость снимка — 78 пикселей, или 9,4^o; помня, что расстояние до неё 12 м, находим высоту проекции стойки 2*12*tg(9,4/2)=2,0 м. Аналогично находим горизонтальную проекцию: 0,8 м. Длину опоры найдём из карты: расстояние от плоскости нашей проекции до верхней точки (обозначена на карте фиолетовым крестиком) 22 пикселя, или 0,9 м, следовательно, полная длина опоры будет (2,0²+0,8²+0,9²)^1/2=2,3 м. На втором кадре вертикальная проекция фрагмента опоры на плоскость снимка 1,6 м, горизотнальная — 1,1 м, расстояние от проекции до верхней точки (по карте) — 0,7 м; следовательно, полная длина фрагмента будет (1,6²+1,1²+0,7²)^1/2=2,1 м. Никакого противоречия не наблюдается: во втором кадре опора видна почти целиком, лишь её маленький (верхний) фрагмент выходит за край кадра. И действительно, измеряя углы на карте, можно убедиться, что верхняя точка опоры выходит за пределы кадра примерно на 2^o (угол между центром кадра, фотографом и верхней точкой — 29^o, тогда как полуугол зрения камеры — 27^o). Поэтому самые верхние несколько (десятков) сантиметров опоры в кадре не видны.

Следовательно, и здесь мы не находим никакого противоречия. «Так какого же роста был астронавт Олдрин?» — спрашиваем мы у Бацуры.

Первый из предложенных Бацурой снимков успел пасть жертвой и другого «реконструктора», о чём мы уже упоминали выше (В. Ростов, «Секретные исследования», http://skyzone.al.ru/space/usa_moon.html ). Разумеется, здесь мы имеем дело с тем же игнорированием законов перспективы. Займёмся собственной реконструкцией.

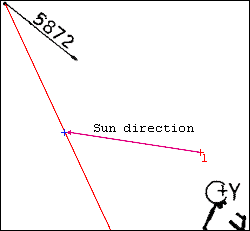Полуугол зрения камеры — 27^o. Обозначим правый край кадра на карте, отложив под таким углом красную линию вправо от направления стрелки. Как мы уже нашли ранее, Олдрин находится в 10,4 м от фотографа. К сожалению, у нас отсутствуют ориентиры для того, чтобы определить расстояние до тени на краю кадра, поэтому придётся воспользоваться косвенным методом. Предположим, что высота фотоаппарата над поверхностью — 1,4 м (фотоаппарат на груди у фотографа). Тогда угол между горизонталью кадра, на которой стоит Олдрин, фотоаппаратом и вертикалью (с вершиной на фотоаппарате) будет arctg(10,4/1,4)=82^o. Не забудем, что все точки, лежащие в кадре на одной горизонтали, отстоят от фотографа на одно и то же расстояние: горизонталь в кадре соответствует «на натуре» кругу с центром в точке фотографирования. Измеренное по снимку параллельно краю кадра, расстояние от горизонтали ног Олдрина до тени на краю кадра составляет около 40 пикселей, то есть 4,8^o. Следовательно, угол между горизонталью тени, фотоаппаратом и вертикалью равен 82^o-4,8^o=77,2^o. Отсюда находим расстояние до тени на краю кадра: 1,4*tg(77,2)=6 м. (Следует заметить, что, поскольку при расчёте мы имели дело с малыми углами, наше определение может быть весьма неточным: возможна ошибка полтора метра и более.) Синим крестиком обозначим на карте точку, отстоящую на красной линии на 6 м от точки съёмки. Этот крестик и соответствует положению тени на краю кадра. Определив положение солнца по карте (см. полноразмерный вариант ), можно убедиться, что наша оценка направления тени весьма близка к реальности.

Вот теперь мы можем измерить длину тени, просто определив расстояние между двумя крестиками. Оно оказывается равным 138 пикселям, или 6 м. Предположив, что ошибка при определении положения тени была 2 м, можно найти по карте, что длина тени лежит в пределах 5 — 7 м. Далее уже не составляет труда найти высоту солнца. В кадр попала не вся тень, а лишь часть её; можно допустить, что в кадре тень нижних 1,5 м от полной высоты фигуры астронавта. Для угла солнца мы найдём тогда arctg(1,5/6)=14^o, с учётом ошибок — 12^o — 17^o. Как известно, в момент прилунения модуля солнце находилось в 10,8^o над горизонтом, астронавты покинули модуль через 6,5 часов после прилунения. Лунные сутки длятся около 29,5 дней (синодический месяц), или 710 часов, прилунение произошло вблизи экватора, следовательно, за 6,5 часов солнце поднялось над горизонтом дополнительно на 360*6,5/710=3,3^o, и его высота в момент съёмки была около 14^o.

Итак, вместо абсурдных 26^o мы получили 12^o — 17^o. Действительная высота солнца была около 14^o, что согласуется в пределах ошибок с нашей грубой оценкой.